Merge Sort Algorithm Explained - Data Structure & Algorithms Tutorials

Merge Sort Algorithm Explained !

Merge Sort is a very popular sorting algorithm, It basically works on dividing an given array into subarrays, and further. Then it sorts the subarrays and merges until the original array is sorted.

So basically if we want to create an efficient sorting algorithm, we have to be able to reorder elements that are in different parts of the array. There are several such sorting algorithms that work on the O(n logn) Time Complexity. A very popular of them is merge sort algorithm, which is based on recursion. We can even solve using iterative method but it gets time consuming and lol yeah lengthy too !

How does Merge Sort Algorithm Works ?

Merge Sort sorts a subarray array[ a . . . b ] as follows:

If a=b, do not do anything, as a=b is nothing but the array has only one element inside it. Which means its already sorted.
Calculate the position of the middle element: k =[(a+b)/2].
Recursively Sort the subarray array[ a . . . k ].
Now Recursively Sort the subarray array[ k+1 . . . b ].
Finally now Merge the sorted subarrays array[ a . . . k ] and array[ k+1 . . . b ] into a sorted subarray array[ a . . . b ].

Divide & Conquer Strategy

Both merge sort and quicksort employ a common algorithmic paradigm based on recursion. This paradigm, divide-and-conquer, breaks a problem into subproblems that are similar to the original problem, recursively solves the subproblems, and finally combines the solutions to the subproblems to solve the original problem. Because divide-and-conquer solves subproblems recursively, each subproblem must be smaller than the original problem, and there must be a base case for subproblems.

You should think of a divide-and-conquer algorithm as having three parts:

Divide the problem into a number of subproblems that are smaller instances of the same problem.
Conquer the subproblems by solving them recursively. If they are small enough, solve the subproblems as base cases.
Combine the solutions to the subproblems into the solution for the original problem.

You can easily remember the steps of a divide-and-conquer algorithm as divide, conquer, combine.

Merge Sort Algorithm

Merge Sort is an efficient algorithm, because it halves the size of the subarray at each step. Then, it merges the sorted subarrays which is possible in linear time, because they are already sorted. Since there are O( logn ) recursive levels, and processing each level takes a total of O( n ) time, the algorithm works in O( n logn ) time.

Illustration

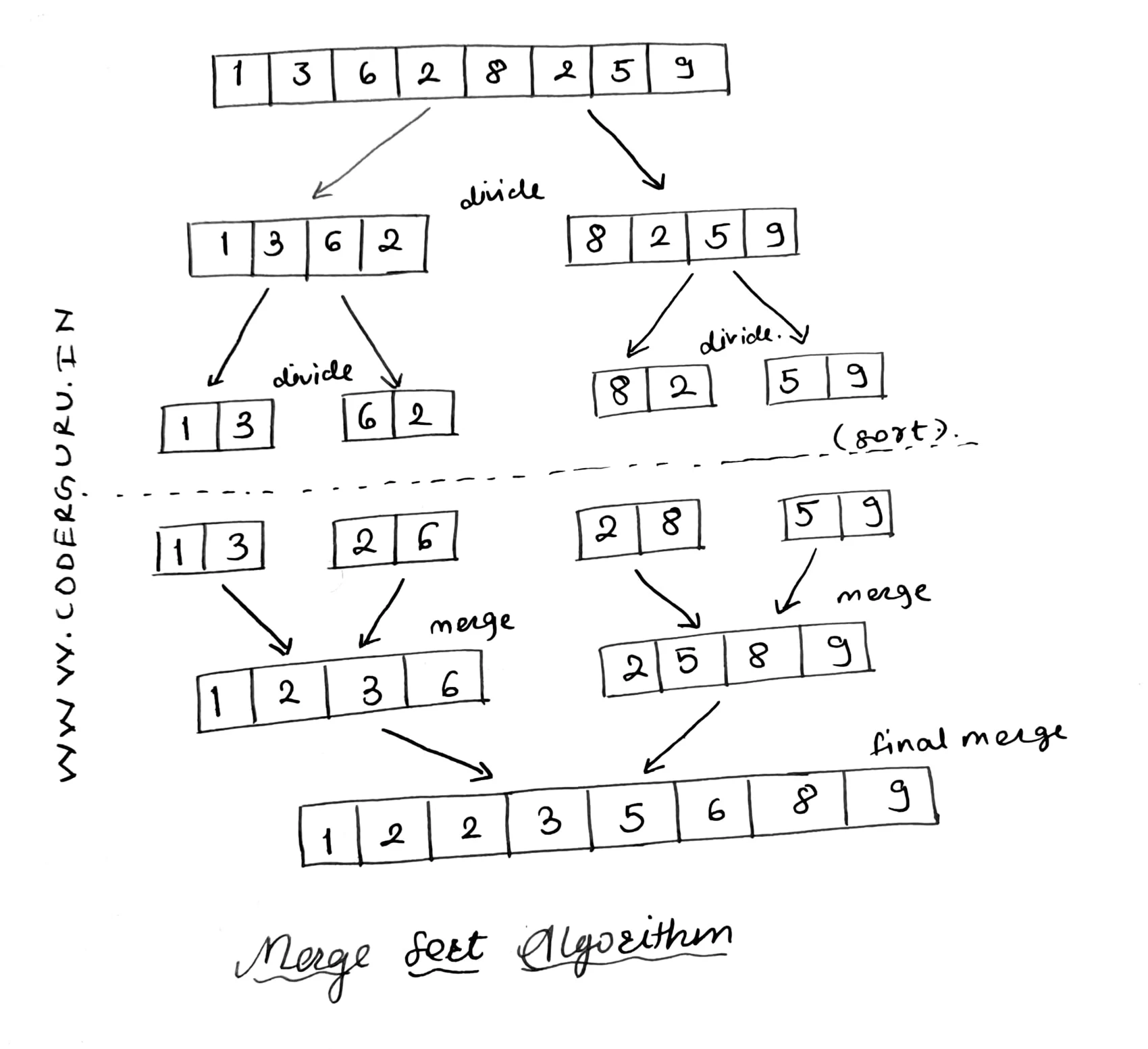Merge Sort Algorithm Tracing

Code Implementation

C++ Source Code to copy this code double click on the codebox

// C++ program for Merge Sort
#include 
using namespace std;

// Merges two subarrays of array[].
// First subarray is arr[begin..mid]
// Second subarray is arr[mid+1..end]
void merge(int array[], int const left, int const mid,
		int const right)
{
	int const subArrayOne = mid - left + 1;
	int const subArrayTwo = right - mid;

	// Create temp arrays
	auto *leftArray = new int[subArrayOne],
		*rightArray = new int[subArrayTwo];

	// Copy data to temp arrays leftArray[] and rightArray[]
	for (auto i = 0; i < subArrayOne; i++)
		leftArray[i] = array[left + i];
	for (auto j = 0; j < subArrayTwo; j++)
		rightArray[j] = array[mid + 1 + j];

	auto indexOfSubArrayOne = 0, indexOfSubArrayTwo = 0;
	int indexOfMergedArray = left;

	// Merge the temp arrays back into array[left..right]
	while (indexOfSubArrayOne < subArrayOne
		&& indexOfSubArrayTwo < subArrayTwo) {
		if (leftArray[indexOfSubArrayOne]
			<= rightArray[indexOfSubArrayTwo]) {
			array[indexOfMergedArray]
				= leftArray[indexOfSubArrayOne];
			indexOfSubArrayOne++;
		}
		else {
			array[indexOfMergedArray]
				= rightArray[indexOfSubArrayTwo];
			indexOfSubArrayTwo++;
		}
		indexOfMergedArray++;
	}

	// Copy the remaining elements of
	// left[], if there are any
	while (indexOfSubArrayOne < subArrayOne) {
		array[indexOfMergedArray]
			= leftArray[indexOfSubArrayOne];
		indexOfSubArrayOne++;
		indexOfMergedArray++;
	}

	// Copy the remaining elements of
	// right[], if there are any
	while (indexOfSubArrayTwo < subArrayTwo) {
		array[indexOfMergedArray]
			= rightArray[indexOfSubArrayTwo];
		indexOfSubArrayTwo++;
		indexOfMergedArray++;
	}
	delete[] leftArray;
	delete[] rightArray;
}

// begin is for left index and end is right index
// of the sub-array of arr to be sorted
void mergeSort(int array[], int const begin, int const end)
{
	if (begin >= end)
		return;

	int mid = begin + (end - begin) / 2;
	mergeSort(array, begin, mid);
	mergeSort(array, mid + 1, end);
	merge(array, begin, mid, end);
}

// UTILITY FUNCTIONS
// Function to print an array
void printArray(int A[], int size)
{
	for (int i = 0; i < size; i++)
		cout << A[i] << " ";
	cout << endl;
}

// Driver code
int main()
{
	int arr[] = { 12, 11, 13, 5, 6, 7 };
	int arr_size = sizeof(arr) / sizeof(arr[0]);

	cout << "Given array is \n";
	printArray(arr, arr_size);

	mergeSort(arr, 0, arr_size - 1);

	cout << "\nSorted array is \n";
	printArray(arr, arr_size);
	return 0;
}

// This code is contributed by Mayank Tyagi
// This code was revised by Joshua Estes

Java Source Code to copy this code double click on the codebox

// Java program for Merge Sort
import java.io.*;

class MergeSort {

	// Merges two subarrays of arr[].
	// First subarray is arr[l..m]
	// Second subarray is arr[m+1..r]
	void merge(int arr[], int l, int m, int r)
	{
		// Find sizes of two subarrays to be merged
		int n1 = m - l + 1;
		int n2 = r - m;

		// Create temp arrays
		int L[] = new int[n1];
		int R[] = new int[n2];

		// Copy data to temp arrays
		for (int i = 0; i < n1; ++i)
			L[i] = arr[l + i];
		for (int j = 0; j < n2; ++j)
			R[j] = arr[m + 1 + j];

		// Merge the temp arrays

		// Initial indices of first and second subarrays
		int i = 0, j = 0;

		// Initial index of merged subarray array
		int k = l;
		while (i < n1 && j < n2) {
			if (L[i] <= R[j]) {
				arr[k] = L[i];
				i++;
			}
			else {
				arr[k] = R[j];
				j++;
			}
			k++;
		}

		// Copy remaining elements of L[] if any
		while (i < n1) {
			arr[k] = L[i];
			i++;
			k++;
		}

		// Copy remaining elements of R[] if any
		while (j < n2) {
			arr[k] = R[j];
			j++;
			k++;
		}
	}

	// Main function that sorts arr[l..r] using
	// merge()
	void sort(int arr[], int l, int r)
	{
		if (l < r) {

			// Find the middle point
			int m = l + (r - l) / 2;

			// Sort first and second halves
			sort(arr, l, m);
			sort(arr, m + 1, r);

			// Merge the sorted halves
			merge(arr, l, m, r);
		}
	}

	// A utility function to print array of size n
	static void printArray(int arr[])
	{
		int n = arr.length;
		for (int i = 0; i < n; ++i)
			System.out.print(arr[i] + " ");
		System.out.println();
	}

	// Driver code
	public static void main(String args[])
	{
		int arr[] = { 12, 11, 13, 5, 6, 7 };

		System.out.println("Given array is");
		printArray(arr);

		MergeSort ob = new MergeSort();
		ob.sort(arr, 0, arr.length - 1);

		System.out.println("\nSorted array is");
		printArray(arr);
	}
}
/* This code is contributed by Rajat Mishra */

Python Source Code to copy this code double click on the codebox

# Python program for implementation of MergeSort


def mergeSort(arr):
	if len(arr) > 1:

		# Finding the mid of the array
		mid = len(arr)//2

		# Dividing the array elements
		L = arr[:mid]

		# Into 2 halves
		R = arr[mid:]

		# Sorting the first half
		mergeSort(L)

		# Sorting the second half
		mergeSort(R)

		i = j = k = 0

		# Copy data to temp arrays L[] and R[]
		while i < len(L) and j < len(R):
			if L[i] <= R[j]:
				arr[k] = L[i]
				i += 1
			else:
				arr[k] = R[j]
				j += 1
			k += 1

		# Checking if any element was left
		while i < len(L):
			arr[k] = L[i]
			i += 1
			k += 1

		while j < len(R):
			arr[k] = R[j]
			j += 1
			k += 1


# Code to print the list
def printList(arr):
	for i in range(len(arr)):
		print(arr[i], end=" ")
	print()


# Driver Code
if __name__ == '__main__':
	arr = [12, 11, 13, 5, 6, 7]
	print("Given array is")
	printList(arr)
	mergeSort(arr)
	print("\nSorted array is ")
	printList(arr)

C Source Code to copy this code double click on the codebox

// C program for Merge Sort
#include 
#include 

// Merges two subarrays of arr[].
// First subarray is arr[l..m]
// Second subarray is arr[m+1..r]
void merge(int arr[], int l, int m, int r)
{
	int i, j, k;
	int n1 = m - l + 1;
	int n2 = r - m;

	// Create temp arrays
	int L[n1], R[n2];

	// Copy data to temp arrays L[] and R[]
	for (i = 0; i < n1; i++)
		L[i] = arr[l + i];
	for (j = 0; j < n2; j++)
		R[j] = arr[m + 1 + j];

	// Merge the temp arrays back into arr[l..r
	i = 0;
	j = 0;
	k = l;
	while (i < n1 && j < n2) {
		if (L[i] <= R[j]) {
			arr[k] = L[i];
			i++;
		}
		else {
			arr[k] = R[j];
			j++;
		}
		k++;
	}

	// Copy the remaining elements of L[],
	// if there are any
	while (i < n1) {
		arr[k] = L[i];
		i++;
		k++;
	}

	// Copy the remaining elements of R[],
	// if there are any
	while (j < n2) {
		arr[k] = R[j];
		j++;
		k++;
	}
}

// l is for left index and r is right index of the
// sub-array of arr to be sorted
void mergeSort(int arr[], int l, int r)
{
	if (l < r) {
		int m = l + (r - l) / 2;

		// Sort first and second halves
		mergeSort(arr, l, m);
		mergeSort(arr, m + 1, r);

		merge(arr, l, m, r);
	}
}

// Function to print an array
void printArray(int A[], int size)
{
	int i;
	for (i = 0; i < size; i++)
		printf("%d ", A[i]);
	printf("\n");
}

// Driver code
int main()
{
	int arr[] = { 12, 11, 13, 5, 6, 7 };
	int arr_size = sizeof(arr) / sizeof(arr[0]);

	printf("Given array is \n");
	printArray(arr, arr_size);

	mergeSort(arr, 0, arr_size - 1);

	printf("\nSorted array is \n");
	printArray(arr, arr_size);
	return 0;
}

Output of the Code is:

Given array is 
12 11 13 5 6 7 
Sorted array is 
5 6 7 11 12 13

Complexity Analysis of Merge Sort:

Time Complexity: We already spoke that for merge sort our time complexity remains O( nlogn ) no matter how the array is given to us. We can derive merge sort's time complexity using recurrence relations.

T(n) = 2T(n/2) + θ(n)

Auxiliary Space: O(N), In merge sort all elements are copied into an auxiliary array. So N auxiliary space is required for merge sort.

Applications of Merge Sort Algorithm

Sorting large datasets: Merge sort is particularly well-suited for sorting large datasets due to its guaranteed worst-case time complexity of O(n log n).
External sorting: Merge sort is commonly used in external sorting, where the data to be sorted is too large to fit into memory.
Custom sorting: Merge sort can be adapted to handle different input distributions, such as partially sorted, nearly sorted, or completely unsorted data.
Inversion Count Problem

Advantages of Merge Sort:

Stability: Merge sort is a stable sorting algorithm, which means it maintains the relative order of equal elements in the input array.
Guaranteed worst-case performance: Merge sort has a worst-case time complexity of O(N logN), which means it performs well even on large datasets.
Parallelizable: Merge sort is a naturally parallelizable algorithm, which means it can be easily parallelized to take advantage of multiple processors or threads.

Drawbacks of Merge Sort:

Space complexity: Merge sort requires additional memory to store the merged sub-arrays during the sorting process.
Not in-place: Merge sort is not an in-place sorting algorithm, which means it requires additional memory to store the sorted data. This can be a disadvantage in applications where memory usage is a concern.
Not always optimal for small datasets: For small datasets, Merge sort has a higher time complexity than some other sorting algorithms, such as insertion sort. This can result in slower performance for very small datasets.

KeyWords & Search :

merge sort time complexity
merge sort algorithm in c
merge sort algorithm python
merge sort pseudocode
merge sort algorithm in steps
quick sort
quick sort algorithm
merge sort program in c
merge sort algorithm in daa
quick sort
merge sort algorithm in data structure
merge sort visualization
merge sort in java w3schools
merge sort leetcode

Merge Sort Algorithm Explained - Data Structure & Algorithms Tutorials | DSA