Home News Contact About Support Blog Tools Base Custom More Logo Friends Partners People Work

Floyd's - Warshall Algorithm Explained - Data Structure & Algorithms Tutorials | DSA

byCoderGuru -
0
Floyd's - Warshall Algorithm
Floyd's - Warshall Algorithm 

 Theory Concept : Floyd's Algorithm

  • Floyd Warshall Algorithm is a famous algorithm.
  • It is used to solve All Pairs Shortest Path Problem.
  • It computes the shortest path between every pair of vertices of the given graph.
  • Floyd Warshall Algorithm is an example of dynamic programming approach.

Advantages-

  • It is extremely simple.
  • It is easy to implement.

Algorithm

PseudoCode to copy this code double click on the codebox
// Algorithm for Floyd's - Warshall
Create a |V| x |V| matrix // It represents the distance between every pair of vertices as given
For each cell (i,j) in M do-
if i = = j
	M[ i ][ j ] = 0 // For all diagonal elements, value = 0
if (i , j) is an edge in E
	M[ i ][ j ] = weight(i,j) // If there exists a direct edge between the vertices, value = weight of edge
else
	M[ i ][ j ] = infinity // If there is no direct edge between the vertices, value = ∞
for k from 1 to |V|
	for i from 1 to |V|
		for j from 1 to |V|
		if M[ i ][ j ] > M[ i ][ k ] + M[ k ][ j ]
			M[ i ][ j ] = M[ i ][ k ] + M[ k ][ j ]

Time Complexity:

  • Floyd Warshall Algorithm consists of three loops over all the nodes.
  • The inner most loop consists of only constant complexity operations.
  • Hence, the asymptotic complexity of Floyd Warshall algorithm is O(n^3).
  • Here, n is the number of nodes in the given graph.

When Floyd Waíshall Algorithm Is Used?

  • Floyd Warshall Algorithm is best suited for dense graphs.
  • This is because its complexity depends only on the number of vertices in the given graph.
  • For sparse graphs, Johnson’s Algorithm is more suitable.

Problem: 

Consider the following directed weighted graph-

Example Graph for Floyd's Warshall Algorithm
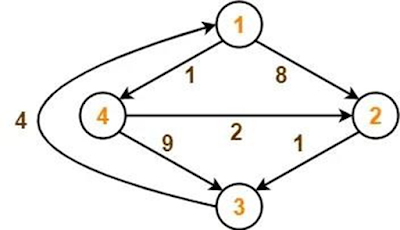Example Graph for Floyd's Warshall Algorithm 
Using Floyd Warshall Algorithm, find the shortest path distance between every pair of vertices.

Solution:

Step-01:

  • Remove all the self loops and parallel edges (keeping the lowest weight edge) from the graph.
In the given graph, there are neither self edges nor parallel edges.

Step-02:

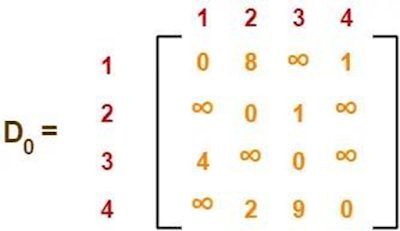
  • Write the initial distance matrix.
  • It represents the distance between every pair of vertices in the form of given weights.
  • For diagonal elements (representing self-loops), distance value = 0.
  • For vertices having a direct edge between them, distance value = weight of that edge.
  • For vertices having no direct edge between them, distance value = ∞.
Initial distance matrix for the given graph is-
Distance Matrix - D0
Distance Matrix - D0

Step-03:

Using Floyd Warshall Algorithm, write the following 4 matrices-

The last matrix D4 represents the shortest path distance between every pair of vertices.

Code Implementation 

C++ Code to copy this code double click on the codebox
// C++ Program for Floyd Warshall Algorithm
#include <bits/stdc++.h>
using namespace std;

// Number of vertices in the graph
#define V 4

/* Define Infinite as a large enough
value.This value will be used for
vertices not connected to each other */
#define INF 99999

// A function to print the solution matrix
void printSolution(int dist[][V]);

// Solves the all-pairs shortest path
// problem using Floyd Warshall algorithm
void floydWarshall(int dist[][V])
{

	int i, j, k;

	/* Add all vertices one by one to
	the set of intermediate vertices.
	---> Before start of an iteration,
	we have shortest distances between all
	pairs of vertices such that the
	shortest distances consider only the
	vertices in set {0, 1, 2, .. k-1} as
	intermediate vertices.
	----> After the end of an iteration,
	vertex no. k is added to the set of
	intermediate vertices and the set becomes {0, 1, 2, ..
	k} */
	for (k = 0; k < V; k++) {
		// Pick all vertices as source one by one
		for (i = 0; i < V; i++) {
			// Pick all vertices as destination for the
			// above picked source
			for (j = 0; j < V; j++) {
				// If vertex k is on the shortest path from
				// i to j, then update the value of
				// dist[i][j]
				if (dist[i][j] > (dist[i][k] + dist[k][j])
					&& (dist[k][j] != INF
						&& dist[i][k] != INF))
					dist[i][j] = dist[i][k] + dist[k][j];
			}
		}
	}

	// Print the shortest distance matrix
	printSolution(dist);
}

/* A utility function to print solution */
void printSolution(int dist[][V])
{
	cout << "The following matrix shows the shortest "
			"distances"
			" between every pair of vertices \n";
	for (int i = 0; i < V; i++) {
		for (int j = 0; j < V; j++) {
			if (dist[i][j] == INF)
				cout << "INF"
					<< " ";
			else
				cout << dist[i][j] << " ";
		}
		cout << endl;
	}
}

// Driver's code
int main()
{
	/* Let us create the following weighted graph
			10
	(0)------->(3)
		|	 /|\
	5 |	 |
		|	 | 1
	\|/	 |
	(1)------->(2)
			3	 */
	int graph[V][V] = { { 0, 5, INF, 10 },
						{ INF, 0, 3, INF },
						{ INF, INF, 0, 1 },
						{ INF, INF, INF, 0 } };

	// Function call
	floydWarshall(graph);
	return 0;
}

// This code is contributed by Mythri J L

C Code to copy this code double click on the codebox
// C Program for Floyd Warshall Algorithm
#include <stdio.h>

// Number of vertices in the graph
#define V 4

/* Define Infinite as a large enough
value. This value will be used
for vertices not connected to each other */
#define INF 99999

// A function to print the solution matrix
void printSolution(int dist[][V]);

// Solves the all-pairs shortest path
// problem using Floyd Warshall algorithm
void floydWarshall(int dist[][V])
{
	int i, j, k;

	/* Add all vertices one by one to
	the set of intermediate vertices.
	---> Before start of an iteration, we
	have shortest distances between all
	pairs of vertices such that the shortest
	distances consider only the
	vertices in set {0, 1, 2, .. k-1} as
	intermediate vertices.
	----> After the end of an iteration,
	vertex no. k is added to the set of
	intermediate vertices and the set
	becomes {0, 1, 2, .. k} */
	for (k = 0; k < V; k++) {
		// Pick all vertices as source one by one
		for (i = 0; i < V; i++) {
			// Pick all vertices as destination for the
			// above picked source
			for (j = 0; j < V; j++) {
				// If vertex k is on the shortest path from
				// i to j, then update the value of
				// dist[i][j]
				if (dist[i][k] + dist[k][j] < dist[i][j])
					dist[i][j] = dist[i][k] + dist[k][j];
			}
		}
	}

	// Print the shortest distance matrix
	printSolution(dist);
}

/* A utility function to print solution */
void printSolution(int dist[][V])
{
	printf(
		"The following matrix shows the shortest distances"
		" between every pair of vertices \n");
	for (int i = 0; i < V; i++) {
		for (int j = 0; j < V; j++) {
			if (dist[i][j] == INF)
				printf("%7s", "INF");
			else
				printf("%7d", dist[i][j]);
		}
		printf("\n");
	}
}

// driver's code
int main()
{
	/* Let us create the following weighted graph
			10
	(0)------->(3)
		|		 /|\
	5 |		 |
		|		 | 1
	\|/		 |
	(1)------->(2)
			3		 */
	int graph[V][V] = { { 0, 5, INF, 10 },
						{ INF, 0, 3, INF },
						{ INF, INF, 0, 1 },
						{ INF, INF, INF, 0 } };

	// Function call
	floydWarshall(graph);
	return 0;
}
// This code is contributed by Mythri J L

Java Code to copy this code double click on the codebox
// Java program for Floyd Warshall All Pairs Shortest
// Path algorithm.
import java.io.*;
import java.lang.*;
import java.util.*;

class AllPairShortestPath {
	final static int INF = 99999, V = 4;

	void floydWarshall(int dist[][])
	{

		int i, j, k;

		/* Add all vertices one by one
		to the set of intermediate
		vertices.
		---> Before start of an iteration,
			we have shortest
			distances between all pairs
			of vertices such that
			the shortest distances consider
			only the vertices in
			set {0, 1, 2, .. k-1} as
			intermediate vertices.
		----> After the end of an iteration,
				vertex no. k is added
				to the set of intermediate
				vertices and the set
				becomes {0, 1, 2, .. k} */
		for (k = 0; k < V; k++) {
			// Pick all vertices as source one by one
			for (i = 0; i < V; i++) {
				// Pick all vertices as destination for the
				// above picked source
				for (j = 0; j < V; j++) {
					// If vertex k is on the shortest path
					// from i to j, then update the value of
					// dist[i][j]
					if (dist[i][k] + dist[k][j]
						< dist[i][j])
						dist[i][j]
							= dist[i][k] + dist[k][j];
				}
			}
		}

		// Print the shortest distance matrix
		printSolution(dist);
	}

	void printSolution(int dist[][])
	{
		System.out.println(
			"The following matrix shows the shortest "
			+ "distances between every pair of vertices");
		for (int i = 0; i < V; ++i) {
			for (int j = 0; j < V; ++j) {
				if (dist[i][j] == INF)
					System.out.print("INF ");
				else
					System.out.print(dist[i][j] + " ");
			}
			System.out.println();
		}
	}

	// Driver's code
	public static void main(String[] args)
	{
		/* Let us create the following weighted graph
		10
		(0)------->(3)
		|		 /|\
		5 |		 |
		|		 | 1
		\|/		 |
		(1)------->(2)
		3		 */
		int graph[][] = { { 0, 5, INF, 10 },
						{ INF, 0, 3, INF },
						{ INF, INF, 0, 1 },
						{ INF, INF, INF, 0 } };
		AllPairShortestPath a = new AllPairShortestPath();

		// Function call
		a.floydWarshall(graph);
	}
}

// Contributed by Aakash Hasija

Python Code to copy this code double click on the codebox
# Python3 Program for Floyd Warshall Algorithm

# Number of vertices in the graph
V = 4

# Define infinity as the large
# enough value. This value will be
# used for vertices not connected to each other
INF = 99999

# Solves all pair shortest path
# via Floyd Warshall Algorithm


def floydWarshall(graph):
	""" dist[][] will be the output
	matrix that will finally
		have the shortest distances
		between every pair of vertices """
	""" initializing the solution matrix
	same as input graph matrix
	OR we can say that the initial
	values of shortest distances
	are based on shortest paths considering no
	intermediate vertices """

	dist = list(map(lambda i: list(map(lambda j: j, i)), graph))

	""" Add all vertices one by one
	to the set of intermediate
	vertices.
	---> Before start of an iteration,
	we have shortest distances
	between all pairs of vertices
	such that the shortest
	distances consider only the
	vertices in the set
	{0, 1, 2, .. k-1} as intermediate vertices.
	----> After the end of a
	iteration, vertex no. k is
	added to the set of intermediate
	vertices and the
	set becomes {0, 1, 2, .. k}
	"""
	for k in range(V):

		# pick all vertices as source one by one
		for i in range(V):

			# Pick all vertices as destination for the
			# above picked source
			for j in range(V):

				# If vertex k is on the shortest path from
				# i to j, then update the value of dist[i][j]
				dist[i][j] = min(dist[i][j],
								dist[i][k] + dist[k][j]
								)
	printSolution(dist)


# A utility function to print the solution
def printSolution(dist):
	print("Following matrix shows the shortest distances\
between every pair of vertices")
	for i in range(V):
		for j in range(V):
			if(dist[i][j] == INF):
				print("%7s" % ("INF"), end=" ")
			else:
				print("%7d\t" % (dist[i][j]), end=' ')
			if j == V-1:
				print()


# Driver's code
if __name__ == "__main__":
	"""
				10
		(0)------->(3)
			|		 /|\
		5 |		 |
			|		 | 1
		\|/		 |
		(1)------->(2)
				3		 """
	graph = [[0, 5, INF, 10],
			[INF, 0, 3, INF],
			[INF, INF, 0, 1],
			[INF, INF, INF, 0]
			]
	# Function call
	floydWarshall(graph)
# This code is contributed by Mythri J L

JavaScript JS Code to copy this code double click on the codebox
// A JavaScript program for Floyd Warshall All
	// Pairs Shortest Path algorithm.

	var INF = 99999;
	class AllPairShortestPath {
		constructor() {
		this.V = 4;
		}

		floydWarshall(graph) {
		var dist = Array.from(Array(this.V), () => new Array(this.V).fill(0));
		var i, j, k;

		// Initialize the solution matrix
		// same as input graph matrix
		// Or we can say the initial
		// values of shortest distances
		// are based on shortest paths
		// considering no intermediate
		// vertex
		for (i = 0; i < this.V; i++) {
			for (j = 0; j < this.V; j++) {
			dist[i][j] = graph[i][j];
			}
		}

		/* Add all vertices one by one to
		the set of intermediate vertices.
		---> Before start of a iteration,
			we have shortest distances
			between all pairs of vertices
			such that the shortest distances
			consider only the vertices in
			set {0, 1, 2, .. k-1} as
			intermediate vertices.
		---> After the end of a iteration,
			vertex no. k is added
			to the set of intermediate
			vertices and the set
			becomes {0, 1, 2, .. k} */
		for (k = 0; k < this.V; k++) {
			// Pick all vertices as source
			// one by one
			for (i = 0; i < this.V; i++) {
			// Pick all vertices as destination
			// for the above picked source
			for (j = 0; j < this.V; j++) {
				// If vertex k is on the shortest
				// path from i to j, then update
				// the value of dist[i][j]
				if (dist[i][k] + dist[k][j] < dist[i][j]) {
				dist[i][j] = dist[i][k] + dist[k][j];
				}
			}
			}
		}

		// Print the shortest distance matrix
		this.printSolution(dist);
		}

		printSolution(dist) {
		document.write(
			"Following matrix shows the shortest " +
			"distances between every pair of vertices<br>"
		);
		for (var i = 0; i < this.V; ++i) {
			for (var j = 0; j < this.V; ++j) {
			if (dist[i][j] == INF) {
				document.write(" INF ");
			} else {
				document.write("  " + dist[i][j] + " ");
			}
			}

			document.write("<br>");
		}
		}
	}
	// Driver Code
	/* Let us create the following
		weighted graph
			10
		(0)------->(3)
		|		 /|\
		5 |		 |
		|		 | 1
		\|/		 |
		(1)------->(2)
			3			 */
	var graph = [
		[0, 5, INF, 10],
		[INF, 0, 3, INF],
		[INF, INF, 0, 1],
		[INF, INF, INF, 0],
	];

	var a = new AllPairShortestPath();

	// Print the solution
	a.floydWarshall(graph);
	
	// This code is contributed by rdtaank.

Output
The following matrix shows the shortest distances between every pair of vertices 
      0      5      8      9
    INF      0      3      4
    INF    INF      0      1
    INF    INF    INF      0

KeyWords & Tags:

  • Floyd algorithm code python
  • Floyd algorithm code in c++
  • Floyd algorithm code geeksforgeeks
  • Floyd algorithm code example
  • floyd warshall algorithm
  • floyd's algorithm example
  • floyds algorithm program in c
  • floyd's algorithm in daa
  • order of floyd's algorithm
  • floyd's algorithm in daa
  • floyd's algorithm example
  • floyd's algorithm cycle detection
  • floyd's algorithm in c
  • what is floyd-warshall algorithm
  • floyd-warshall algorithm example with solution
  • warshall algorithm
Tags:
Post a Comment (0)
Previous Post Next Post

About Us

A programmers portal.| Programming Languages | Interview Preparation | Data Structures Algorithm | C++| Java | Python.