Home News Contact About Support Blog Tools Base Custom More Logo Friends Partners People Work

Bubble Sort Algorithm Explained - Data Structure & Algorithms Tutorials | DSA

byCoderGuru -August 22, 2023

0

What is Bubble Sort ?

Bubble Sort, Its a sorting algorithm in which we take two elements from array which are adjacent and compare them, until sort the entire array.

Bubble Sort Algorithm Explained - Data Structure & Algorithms Tutorials | DSA

Bubble sort consists of n rounds. On each round, the algorithm iterates through the elements of the array. Whenever two consecutive elements are found that are not in correct order, the algorithm swaps them.

How does Bubble Sort works ?

We traverse the array from left and compare adjacent elements and the higher one is placed at right side. In this way, the largest element is moved to the rightmost end at first. This process is then continued to find the second largest and place it and so on until the data is sorted.

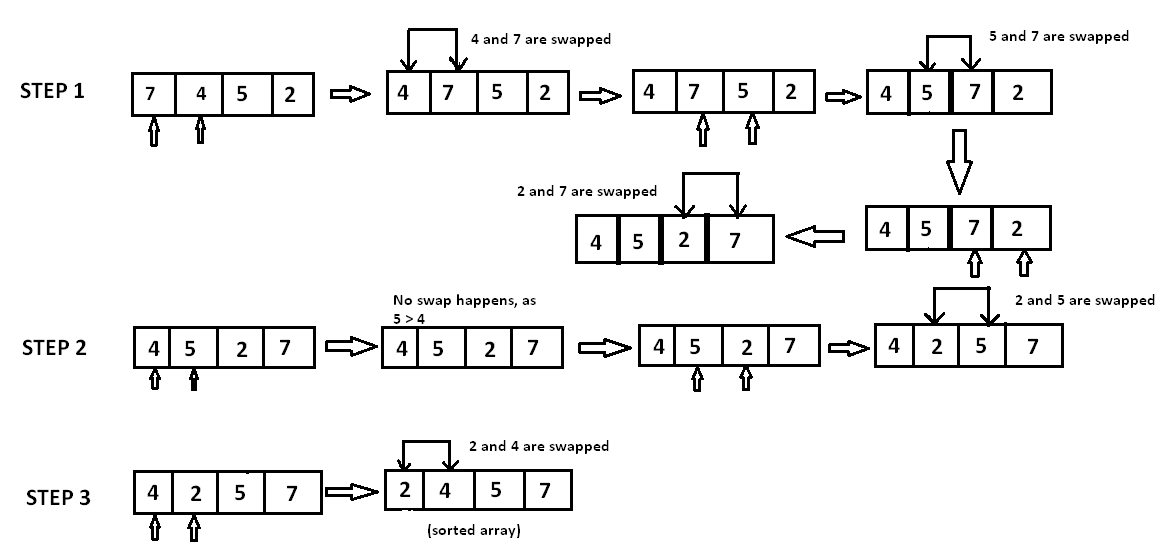Tracing for Bubble Sort

Algorithm

for (int i = 0; i < n; i++) {
    for (int j = 0; j < n-1; j++) {
        if (array[j] > array[j+1]) {
            swap(array[j],array[j+1]);
        }
    }
}

Code Implementation

C++ Source Code to copy this code double click on the codebox

// Optimized implementation of Bubble sort
#include <bits/stdc++.h>
using namespace std;

// An optimized version of Bubble Sort
void bubbleSort(int arr[], int n)
{
	int i, j;
	bool swapped;
	for (i = 0; i < n - 1; i++) {
		swapped = false;
		for (j = 0; j < n - i - 1; j++) {
			if (arr[j] > arr[j + 1]) {
				swap(arr[j], arr[j + 1]);
				swapped = true;
			}
		}

		// If no two elements were swapped
		// by inner loop, then break
		if (swapped == false)
			break;
	}
}

// Function to print an array
void printArray(int arr[], int size)
{
	int i;
	for (i = 0; i < size; i++)
		cout << " " << arr[i];
}

// Driver program to test above functions
int main()
{
	int arr[] = { 64, 34, 25, 12, 22, 11, 90 };
	int N = sizeof(arr) / sizeof(arr[0]);
	bubbleSort(arr, N);
	cout << "Sorted array: \n";
	printArray(arr, N);
	return 0;
}
// This code is contributed by shivanisinghss2110

Java Source Code to copy this code double click on the codebox

// Optimized java implementation of Bubble sort

import java.io.*;

class GFG {
	
	// An optimized version of Bubble Sort
	static void bubbleSort(int arr[], int n)
	{
		int i, j, temp;
		boolean swapped;
		for (i = 0; i < n - 1; i++) {
			swapped = false;
			for (j = 0; j < n - i - 1; j++) {
				if (arr[j] > arr[j + 1]) {
					
					// Swap arr[j] and arr[j+1]
					temp = arr[j];
					arr[j] = arr[j + 1];
					arr[j + 1] = temp;
					swapped = true;
				}
			}

			// If no two elements were
			// swapped by inner loop, then break
			if (swapped == false)
				break;
		}
	}

	// Function to print an array
	static void printArray(int arr[], int size)
	{
		int i;
		for (i = 0; i < size; i++)
			System.out.print(arr[i] + " ");
		System.out.println();
	}

	// Driver program
	public static void main(String args[])
	{
		int arr[] = { 64, 34, 25, 12, 22, 11, 90 };
		int n = arr.length;
		bubbleSort(arr, n);
		System.out.println("Sorted array: ");
		printArray(arr, n);
	}
}

// This code is contributed
// by Nikita Tiwari.

Python Source Code to copy this code double click on the codebox

# Python program for implementation of MergeSort


# Optimized Python program for implementation of Bubble Sort


def bubbleSort(arr):
	n = len(arr)
	
	# Traverse through all array elements
	for i in range(n):
		swapped = False

		# Last i elements are already in place
		for j in range(0, n-i-1):

			# Traverse the array from 0 to n-i-1
			# Swap if the element found is greater
			# than the next element
			if arr[j] > arr[j+1]:
				arr[j], arr[j+1] = arr[j+1], arr[j]
				swapped = True
		if (swapped == False):
			break


# Driver code to test above
if __name__ == "__main__":
	arr = [64, 34, 25, 12, 22, 11, 90]

	bubbleSort(arr)

	print("Sorted array:")
	for i in range(len(arr)):
		print("%d" % arr[i], end=" ")

C Source Code to copy this code double click on the codebox

// Optimized implementation of Bubble sort
#include <stdbool.h>
#include <stdio.h>

void swap(int* xp, int* yp)
{
	int temp = *xp;
	*xp = *yp;
	*yp = temp;
}

// An optimized version of Bubble Sort
void bubbleSort(int arr[], int n)
{
	int i, j;
	bool swapped;
	for (i = 0; i < n - 1; i++) {
		swapped = false;
		for (j = 0; j < n - i - 1; j++) {
			if (arr[j] > arr[j + 1]) {
				swap(&arr[j], &arr[j + 1]);
				swapped = true;
			}
		}

		// If no two elements were swapped by inner loop,
		// then break
		if (swapped == false)
			break;
	}
}

// Function to print an array
void printArray(int arr[], int size)
{
	int i;
	for (i = 0; i < size; i++)
		printf("%d ", arr[i]);
}

// Driver program to test above functions
int main()
{
	int arr[] = { 64, 34, 25, 12, 22, 11, 90 };
	int n = sizeof(arr) / sizeof(arr[0]);
	bubbleSort(arr, n);
	printf("Sorted array: \n");
	printArray(arr, n);
	return 0;
}

Output of the Code is:

Sorted array:  11 12 22 25 34 64 90

Complexity Analysis of Merge Sort:

Time Complexity:

Best Case: The best case occurs when the array is already sorted. So the number of comparisons required is N-1 and the number of swaps required = 0. Hence the best case complexity is O(N).
Worst Case: The worst-case condition for bubble sort occurs when elements of the array are arranged in decreasing order. In the worst case, the total number of iterations or passes required to sort a given array is (N-1). where ‘N’ is the number of elements present in the array.
Average Case Time Complexity: The number of comparisons is constant in Bubble Sort. So in average case, there are O(N2) comparisons. This is because irrespective of the arrangement of elements, the number of comparisons C(N) is same.

Auxiliary Space:

O(1) as no additional space is used.

Advantages of Bubble Sort

The primary advantage of the bubble sort is that it is popular and easy to implement.
In the bubble sort, elements are swapped in place without using additional temporary storage.
The space requirement is at a minimum

Disdvantages of Bubble Sort

The main disadvantage of the bubble sort is the fact that it does not deal well with a list containing a huge number of items.
The bubble sort requires n-squared processing steps for every n number of elements to be sorted.
The bubble sort is mostly suitable for academic teaching but not for real-life applications.

KeyWords

bubble sort best case time complexity

selection sort

insertion sort

bubble sort time complexity

bubble sort algorithm in c

bubble sort algorithm python

bubble sort pseudocode

bubble sort algorithm in steps

quick sort

quick sort algorithm

bubble sort program in c

bubble sort algorithm in daa

quick sort

bubble sort algorithm in data structure

bubble sort visualization

bubble sort in java w3schools

bubble sort leetcode